- 19 مارس 2024
- admin
محاسبه پیشرفت فعالیت با اجرای Step %Complete در نرم افزار پریماورا
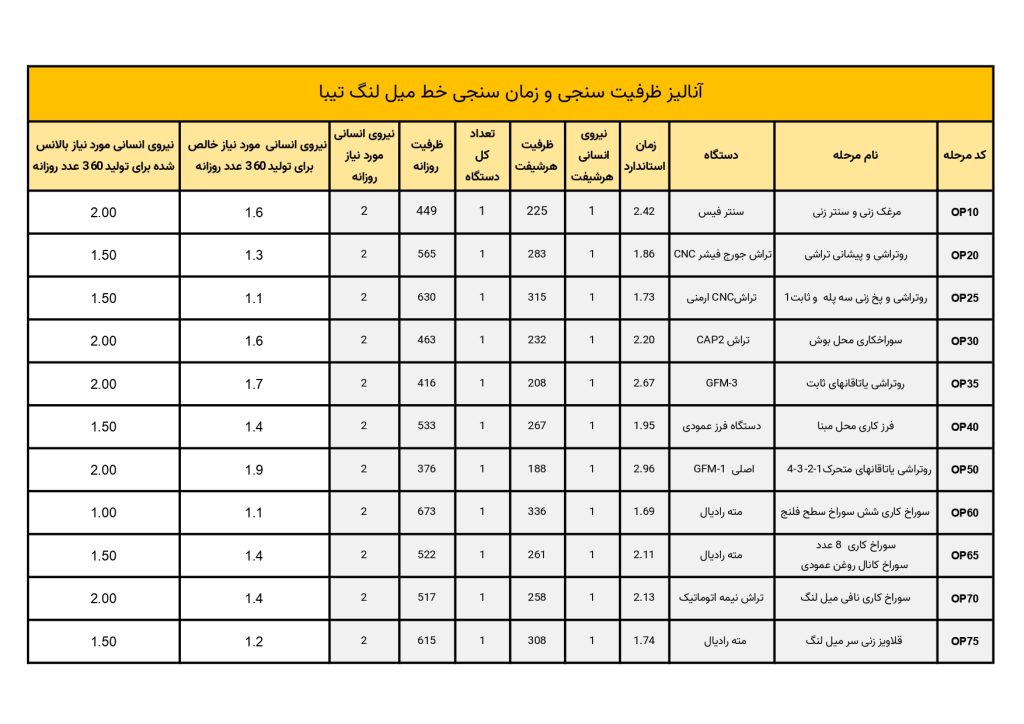
محاسبه پیشرفت فعالیتهای پریماورا با اجرای Step%Complete پروژه ای فرضی با نام Step% Complete تعریف کرده و مشخصات زیر در نظر بگیرید:تاریخ شروع پروژه 4 مارس 2024 و تقویم کاری Standard 5 Day Workweek را از پیش فرض سیستم انتخاب ...